The third of the Korg opsix firmware 2.0 effect operators that I’m covering in this series is the Comb filter effect operator. Related to the Short delay operator, the Comb filter is well suited to physical modelling of sounds.

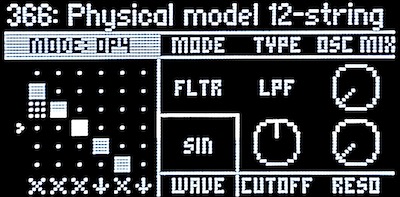
Block diagram

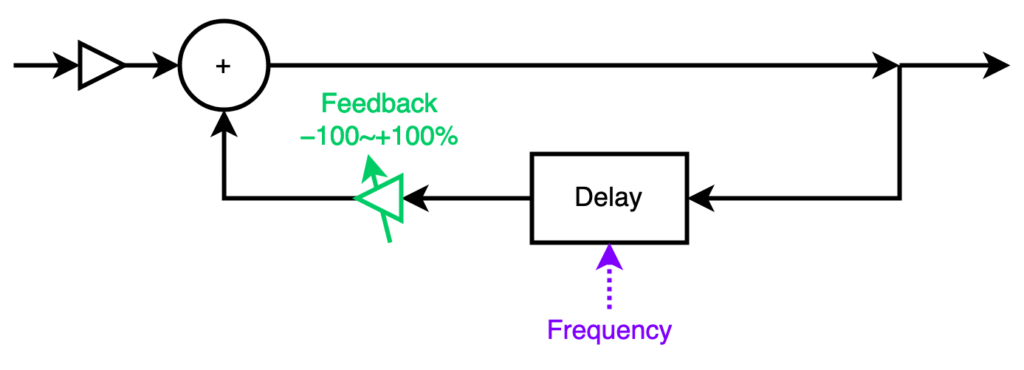
Names are complicated! Didn’t I say that the Short delay effect operator is a comb filter? (It is.) So what’s the Comb filter operator for, then?

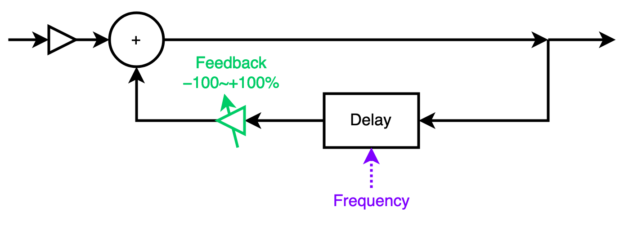
Well, there are two kinds of comb filter: a feedforward form and a feedback form. The Short delay operator is a feedforward comb filter, where the delayed signal is simply added to the output, and the Comb filter operator is a feedback comb filter, where the delayed signal is added back to the input and thence re-enters the delay.

The two types of comb filter share the characteristic repeated pattern in their frequency responses that give them their name, but the shapes are different: feedforward comb filters (including flangers) have notches in their frequency response; feedback comb filters like the Comb filter operator have spikes in their frequency response.

Physical modelling

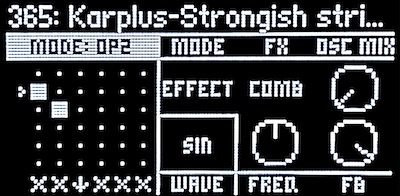
Modification knob F controls Feedback, that is, how much of the delayed signal is added back to the input. When set to 0%, the Comb filter operator is indistinguishable from a simple bypass (self-evident from the block diagram above). For values up to 100%, feedback emphasizes the frequencies f, 2f, 3f, etc., (i.e., every harmonic) more and more. Near 100% feedback, the sound is self-sustaining, even if the input signal is no longer present. (I don’t think “100% feedback” is really 100%, because if it was, the spikes would be infinitely high, infinitely narrow, and the sound would never decay.) It is in this near-unity feedback region that the Comb filter operator is most useful.

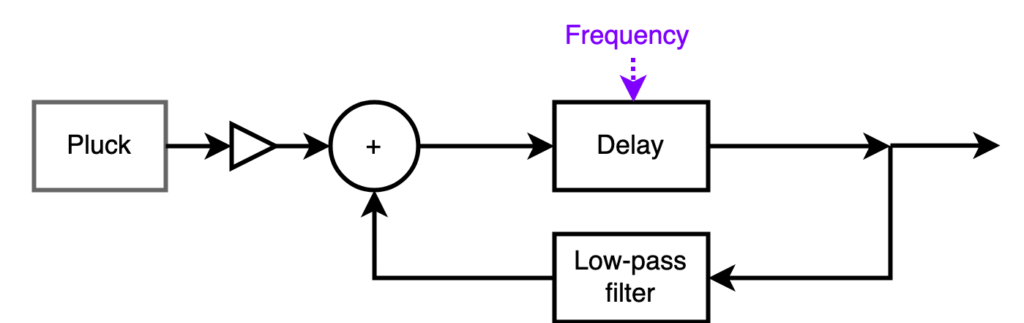
In the Comb filter operator, the length of the delay tracks frequency of the played note, similar to what happens in the Phaser and Filter and other operators. This is in contrast to the Short delay operator, in which you dial up the delay in milliseconds. I lamented the inability of the Short delay operator to track the keyboard, as it prevented the implementation of a Karplus-Strong model plucked string. Can you do a Karplus-Strong string with the Comb filter effect operator? Almost.

The Karplus-Strong model is strictly a filtered-feedback comb filter, with a light filtering stage inside the feedback loop that the opsix’s Comb filter operator lacks. This filter corresponds to losses in the reflection at the end of the string; without it, the timbre of the plucked string stays uncharacteristically bright.

What to do? Cheat. Put a filter after the feedback loop instead of inside, with an envelope that sweeps the cutoff frequency from high to low. This is not strictly physical modelling any more, rather, it’s just old-school subtractive synthesis, but it’s really hard to hear the difference.

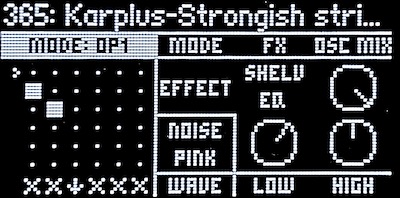
The following sample simulates a string instrument. Operator 1 is a very short (20 ms) burst of noise. The new Pink noise waveform is a good choice, enhanced a bit in the bass with the Shelving Equalizer effect operator. Operator 2 is the Comb filter. Its waveform is immaterial because the oscillator mix is set to zero. A feedback of close to 100% provides a nice stringlike decay. Operator 3 is a simple lowpass filter with a fairly high cutoff.

Playing with feedback

The Feedback modification knob (F) can also be turned below 0%, down to −100%. At negative feedback values, the signal is inverted before being added back to the input. Interestingly, this does not change the shape of the spikes in the frequency response; it just shifts them by −f/2: with negative feedback, the frequencies emphasized are f/2, 3f/2, 5f/2, etc., which to the ear sounds like a note one octave lower along with only the odd harmonics.

Odd-only harmonics correspond to instruments made with a vibrating cantilever fixed at one end, such as the tines of a music box comb (pun unintended). The following sample also includes a little mixed-in blue noise, which is also comb filtered, adding a bow-like element.

Putting it all together

In these three posts, I have explored how three of the opsix 2.0 firmware’s effect operators can be used to model physical instruments. These effects can be combined into a single patch with great results.

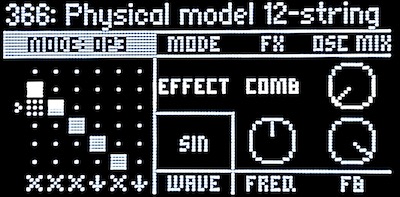
The following sample is a physical model of a 12-string acoustic guitar. It strings (pun intended) together a pluck in operator 1 and a Short delay in operator 2 (acting as a plain short delay, duplicating the pluck as would happen in a 12-string guitar). A mix of operator 1 (the first pluck) and operator 2 (both plucks at equal volume) is made, creating a resulting pair of plucks where the first is louder than the second. These plucks are then fed into a Comb filter in operator 3 to model the string, and a filter in operator 4 to model the loss of brightness over time. Finally, two Phaser operators in operators 5 and 6, at fixed frequencies, to introduce some variation to the frequency response as would happen in an acoustic guitar body. The output is mixed from the filter output and the phaser output, producing a result with subtle notches in the frequency response. Finally, the sound is passed into a traditional chain of effects (chorus, equalizer and reverb).

Conclusion

I do wish that rather than one operator type with ten variants, Korg had added the new operators as first-class citizens, as Filter and Wave folder already are. That would have freed modification knob B to be another per-effect control.

It’s been educational exploring these new effect operators. Their block diagrams, which I had to reverse-engineer, are all quite simple on paper, but the resulting sounds that they produce show a lot of emergent complexity. Of the ten effect operators, I’ve barely touched the Shelving Equalizer and Distortion operators, and haven’t mentioned Peaking Equalizer, Drive, Waveshaper, Decimator, or Punch operators at all. With the 2.0 firmware, the opsix now lives up to the hype of being an “altered” FM synthesizer: it’s possible to make many new exciting sounds without stepping anywhere near FM synthesis.

Part 1: Phaser | Part 2: Short delay | Part 3: Comb filter