In October 2021, Korg released a firmware update for its opsix synthesizer, introducing ten new operator types, a ragtag bundle grouped under the umbrella of “effects”. There isn’t much in common between the ten effects apart from the shared user interface used to configure them. This post is a deep dive into the Phaser effect.

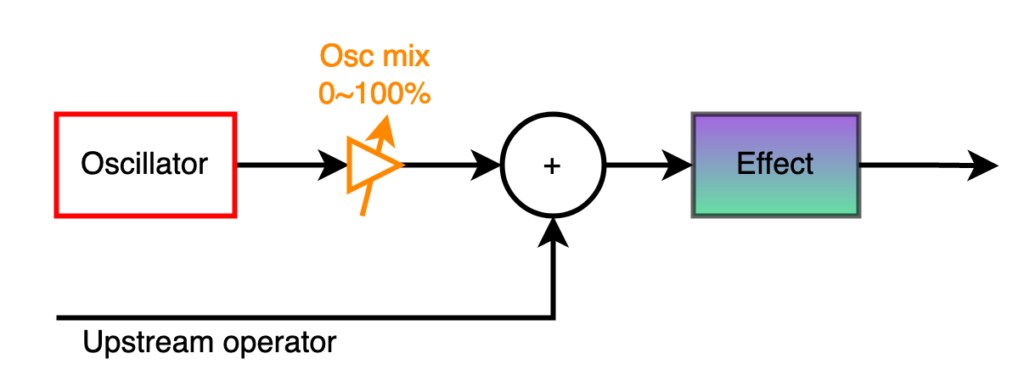
All of the Effect operators have the same overall structure: Input from upstream is added to the current operator’s own oscillator, the latter scalable in volume. The resulting sum is fed into one of ten effects. The output from the effect becomes the output of the operator. It is common for the upstream operator to be absent, or for the current operator’s oscilator to be scaled to zero, making the summation a trivial wire.

A phaser is a notch-reject filter

The phaser effect has been a favourite of musicians for decades. It adds harmonic complexity to a sound by selectively cutting out frequencies in the signal, often at harmonically unrelated frequencies. Often, those frequencies are swept up and down periodically with the use of a low-frequency oscillator (LFO) to give an oily, swishy texture to the sound.

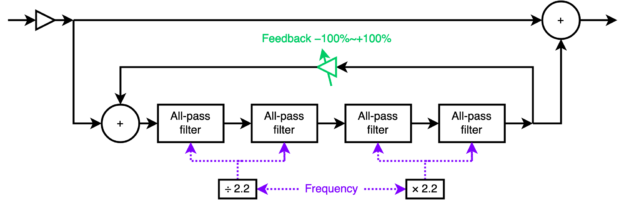
A phaser works by splitting the input signal into a dry and wet component. The wet component is sent through a series of all-pass filters, and then added back to the dry component. An all-pass filter does not change the amplitude of a signal, but it changes the phase of the frequencies in the signal: low frequencies are left unchanged (0º phase change) but high frequencies are delayed so that they are fully out of phase with the input (180º phase change). At the all-pass filter’s “cutoff frequency” (more correctly the quadrature frequency) the phase difference is 90º.

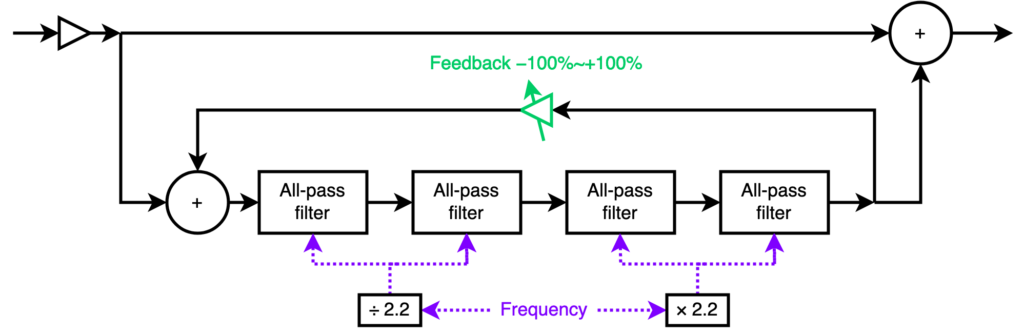
A common arrangement is the four-stage phaser: four all-pass filters in a line. The cumulative effect of a four-stage phaser is that the wet signal will be 4 × 180º = 720º out of phase at high frequencies. 720º is equivalent to 0º (modulo a full cycle of 360º), so adding the wet signal back to the dry signal will constructively interfere. Notably, at certain frequencies in between, the phase difference will pass through 180º and 540º, resulting in two frequencies at which destructive interference completely cancels the signal. In short, a four-stage phaser is a two-frequency notch-reject filter. In general, n × 2 all-pass filter stages produce n notches in the frequency response.

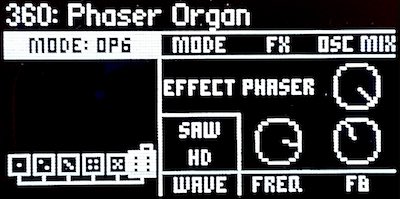
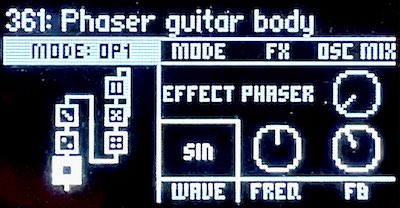
opsix phaser implementation

On the opsix, which is a four-stage phaser, the two phaser notch frequencies track each played note. The all-pass filters are tuned so that one notch is about 15 semitones below the played note’s fundamental frequency, and the other is about 15 semitones above the fundamental. The distance of about 30 semitones (about 2½ octaves) between the notches cannot be changed. Because the frequency ratios are constant, the timbre of the played waveform is consistent no matter what note is played.

With a harmonically rich base waveform like a sawtooth, the Phaser effect can produce new derived waveforms beyond the couple of dozen standard waveforms. Additionally, the modification knob Frequency (knob E) can increase or decrease the frequencies of the notches in lockstep, always the same distance apart, but centred on a frequency other than the fundamental of the played note. It is even possible to almost completely cancel the fundamental frequency by setting the Frequency modification knob to +15 (or −15) semitones. By adjusting the frequency in this way, a range of new waveforms can be created.

The Feedback modification knob (knob F) causes only a subtle change to the frequency response of the Phaser effect, and does not affect the notch frequencies at all. A positive feedback value enhances the frequencies between the two notches, while a negative feedback reduces the entire phaser effect.

The following sample is a modified drawbar organ, with six independent operators, each a saw wave with a different Frequency offset. The resulting tone is richer in harmonics than a traditional sine wave additive organ, but the components are noticeably not simple sawtooth waves.

Combining phasers with LFOs

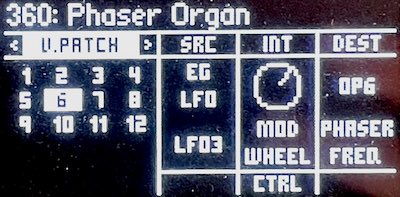
While this sound is interesting, it is not what a musician would customarily consider to be a phaser effect. For one thing, the notch frequencies (for a given note) don’t move over time, so there is no swish. This is easily fixed: add a V.Patch to modify the operator’s Frequency with an LFO. It’s even possible to stack LFOs on a single operator, or to apply different LFOs to different operators to achieve a crossfadey beat-like effect.

The following sample introduces three LFOs applied to the six standalone operators. The LFOs have different periods so there is a subtle beat.

Disabling key tracking

So far, all of these uses of the Phaser effect operator have used the key tracking feature built into the effect. In some cases, this isn’t desirable, and you want the phaser to have notches that are constant no matter what note is played. This can be done by setting the operator’s pitch mode to Fixed. This only disables the key tracking: the Frequency modification knob works in the same way, and can still be swept with an LFO.

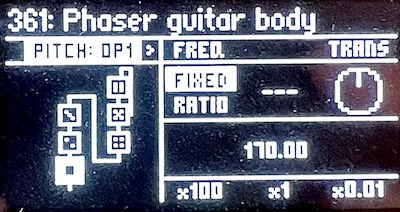
The following sample strings three Phaser effects in series to produce a six-notch phaser effect, with the same frequency response for all played notes. Careful adjustments to the notch frequencies using the ratio knobs can produce a result reminiscent of a guitar body, with several dead frequencies caused by destructive interference.

Conclusion

I hasten to add that the 1.0 firmware’s standard Phaser postprocessing effect is still present and can be assigned to one of the three effect slots. It has the advantage that it does not use up an operator, It is a stereo effect with the LFO applied differently to left and right channels, you can control the wet/dry mix, and you can tie the LFO to the tempo of the music. If all you need is a traditional oily phaser effect with an LFO on top, you should keep using this.

Rather, the Phaser operator effect is a building block that you can add to your repertoire to move beyond the standard waveforms and to add elements of physical modelling to your patches. The latter is a theme that I will return to in my next installment when I cover the Short Delay operator effect.

Part 1: Phaser | Part 2: Short delay | Part 3: Comb filter